How to Calculate Percent Error: A Comprehensive Guide with Formulas, Examples

Understanding how to calculate percent error is a critical skill for scientists, engineers, students, and professionals across industries. It helps assess the accuracy of experimental results, measurements, and predictions by comparing them to accepted or true values.

Whether you’re conducting a lab experiment, calibrating equipment, or analyzing data, this guide will walk you through the percent error formula, provide real-world examples, and explain its importance in various fields.

What is Percent Error?

Percent error is a statistical measure that quantifies the difference between a measured (experimental) value and a true (accepted) value, expressed as a percentage. It answers the question: “How far off is my result from the expected value?”

The percent error formula is:

This formula ensures that the result is always positive, regardless of whether the experimental value is higher or lower than the true value.

Why Percent Error Matters

Percent error is widely used in various fields to ensure accuracy and reliability. Here’s why it’s important:

1. Scientific Research:
   • Labs use percentage error to validate hypotheses and ensure the reliability of experimental data.
   • For example, in chemistry, a reaction yield with a percent error of less than 5% is often considered acceptable.
2. Quality Control:
   • Industries like pharmaceuticals and manufacturing rely on error calculation to maintain product standards.
   • A drug’s active ingredient must be within 1% error of the stated dose to ensure patient safety.
3. Education:
   • Students learn how to calculate percentage error to improve experimental accuracy and understand the importance of precision in scientific measurements.
4. Data Analysis:
   • In machine learning and data science, percent error is used to evaluate the accuracy of predictive models. For example, a house price prediction model with a percent error of less than 3% is considered highly accurate.

Step-by-Step: How to Calculate Percent Error

Let’s break down the process with detailed examples:

Example 1: Lab Experiment

• True Value: 250 mL (accepted volume of a liquid).
• Experimental Value: 243 mL (measured volume).

Step 1: Subtract the true value from the experimental value.243 mL−250 mL=−7 mL243mL−250mL=−7mL

Step 2: Divide by the true value.

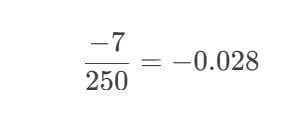
Step 3: Take the absolute value and multiply by 100%.∣−0.028∣×100%=2.8%

Result: The percent error is 2.8%.

Example 2: Physics Experiment

• True Value: 9.8 m/s² (acceleration due to gravity).
• Experimental Value: 9.5 m/s² (measured value).

Step 1: Subtract the true value from the experimental value.

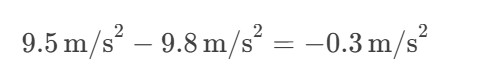
Step 2: Divide by the true value.

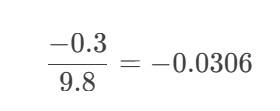
Step 3: Take the absolute value and multiply by 100%.

∣−0.0306∣×100%=3.06%

Result: The percent error is 3.06%.

Real-World Applications of Percent Error

1. Pharmaceutical Manufacturing

• In drug production, the concentration of active ingredients must be within a specific percent error range (often <1%) to ensure safety and efficacy.

2. Climate Science

• Satellite temperature readings with a percent error greater than 5% are recalibrated to ensure accurate climate models and predictions.

3. Automotive Engineering

• Fuel efficiency claims are tested for percentage error to comply with advertising regulations. For example, a car advertised with 30 MPG must achieve within 2% of that value in real-world tests.

4. Machine Learning

• Predictive models are evaluated using percent error to measure accuracy. For instance, a model predicting house prices with a percent error of less than 3% is considered reliable.

Common Mistakes to Avoid

1. Ignoring Absolute Value:
   • Percent error must always be positive. Forgetting absolute value leads to incorrect negative results.
2. Mixing Up Values:
   • Always subtract Experimental – True (not True – Experimental).
3. Rounding Too Early:
   • Wait until the final step to round to maintain precision.
4. Using Incorrect Units:
   • Ensure both experimental and true values are in the same units before calculating.

Percent Error vs. Percent Difference

While percent error compares a measured value to a true value, percent difference compares two experimental values (neither is “true”).

Formula for Percent Difference:

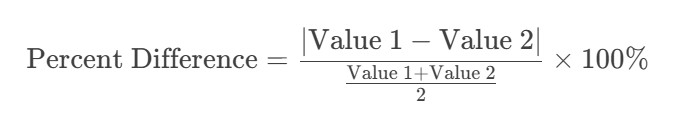
Example:

• Value 1: 50
• Value 2: 55

Calculation:

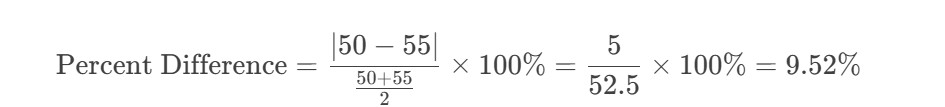
FAQs About Percent Error

Q: Can percent error be negative?

A: No! The absolute value in the percent error formula ensures it’s always positive.

Q: What’s an acceptable percent error?

A: It varies by field. In chemistry, <5% is often acceptable; in engineering, <1% may be required.

Q: How is percent error used in machine learning?

A: It evaluates model accuracy (e.g., predicting house prices within 3% error).

Q: What if the true value is zero?

A: Percent error is undefined (division by zero). Use absolute error instead.

Conclusion

Mastering how to calculate percent error empowers you to critically evaluate data accuracy in experiments, manufacturing, and research. By applying the percent error formula and avoiding common mistakes, you can ensure reliable results. Whether you’re a student, scientist, or professional, understanding percent error is a key step toward achieving precision and credibility in your work.