How to Calculate Percentage: A Comprehensive Guide
Percentages are an integral part of mathematics that we encounter regularly in various aspects of life. Whether calculating discounts, analyzing statistics, or figuring out interest rates, understanding how to calculate percentages quick is essential. This article will walk you through everything you need to know about percentages, including their calculation, applications, and common percentage formulas.
What is Percentage?
A percentage is a way to express a number as a fraction of 100. It represents how much out of 100 parts a particular value is. The symbol “%” is used to denote percentages. For instance, 25% means 25 out of 100, or one-quarter.
The Formula for Percentage Calculation
The formula for calculating a percentage is straightforward:
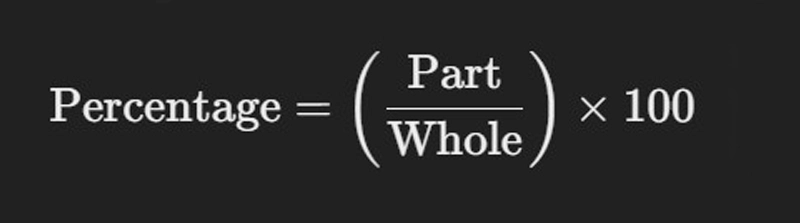
Where:
- Part is the portion of the total you are examining.
- Whole is the total amount or value.
This formula helps compute the percentage for any given part and whole.
How to Calculate Percentage Step by Step
Here, we will break down the calculation of percentages into easy-to-follow steps using real-life examples.
Step 1: Identify the Total Value (Whole)
The first step is identifying the total value or the base from which the percentage will be calculated. For example, let’s say you have 80 students in a class.
Step 2: Determine the Part of the Total
Next, find the part that you want to calculate the percentage for. For example, 20 students scored above 90% on a test.
Step 3: Apply the Percentage Formula
Now, use the formula to calculate the percentage:
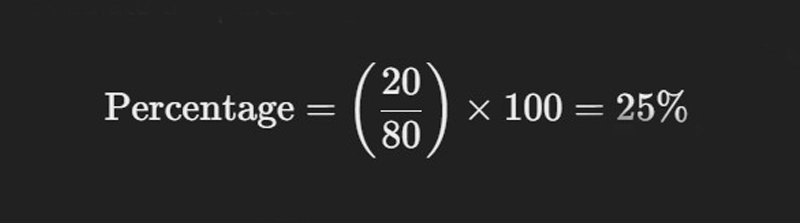
Thus, 25% of the students scored above 90%.
Calculating Percentage from Two Numbers
Sometimes, you might need to calculate the percentage between two numbers directly. This method is used to compare two values.

For instance, if the price of a product increases from $50 to $65, you can calculate the percentage increase as follows:
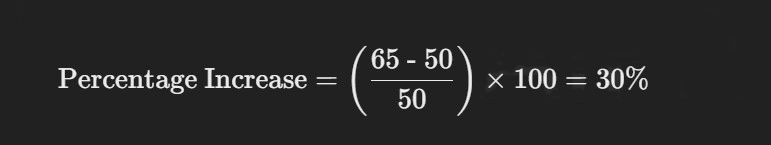
The price has increased by 30%.
How to Calculate Percentage Increase and Decrease
Percentage Increase
When a value increases, the formula for percentage increase is:
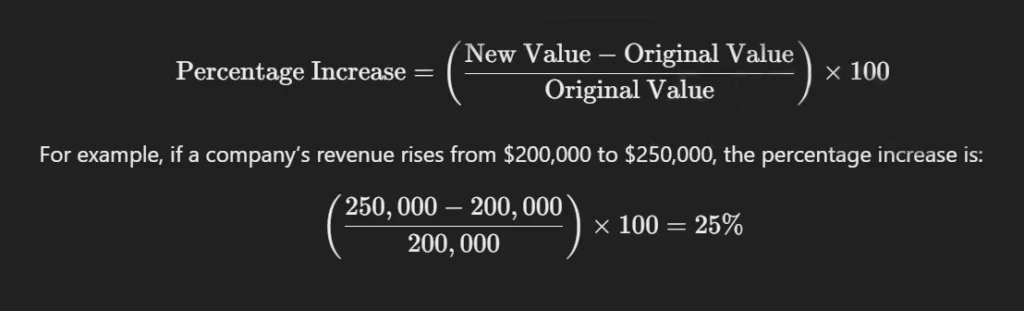
Percentage Decrease
In contrast, the percentage decrease is calculated when a value drops. The formula is:

How to Calculate Percentage of a Number
One common task is calculating the percentage of a specific number. This is useful for determining discounts, interest, or portions of a total.

Real-Life Applications of Percentage
Percentages are used in many real-world scenarios, including:
- Finance: To calculate interest rates, inflation, and tax.
- Shopping: For discounts, sales, and profit margins.
- Statistics: To represent data, growth, and comparisons.
- Education: To compute grades and performance metrics.
- Healthcare: In statistical data for research or patient recovery rates.
Example: Calculating Discount Percentage
If a $100 item is on sale for $75, you can calculate the discount percentage by using the formula:
Discount Percentage=(100−75100)×100=25%
The discount offered is 25%.
Common Percentage Formulas
Below are some common percentage-related formulas that are frequently used:

How to Convert Decimals and Fractions to Percentages
Converting numbers from decimals or fractions into percentages is simple and often necessary.
Decimal to Percentage
To convert a decimal to a percentage, multiply the decimal by 100.
For example, converting 0.75 to a percentage:
0.75×100=75%
Fraction to Percentage
To convert a fraction number to a percentage, divide the numerator by the denominator and multiply by 100.
For example, converting 3/4 to a percentage:
3/4×100=75%
Percentage Word Problems
Below are a couple of common word problems involving percentages and their solutions:
Problem 1: Finding the Percentage of a Quantity
A customer bought 60 apples, and 12 of them were rotten. What percentage of the apples were rotten?
Solution: Percentage=(12/60)×100=20%
Thus, 20% of the apples were rotten.
Problem 2: Calculating a Discount
A $200 jacket is on sale for 20% off. What is the sale price?
Solution: First, find 20% of $200:
Discount=(20/100)×200=40
Now subtract the discount from the original price:
Sale Price=200−40=160
Thus, the jacket is priced at $160 after the discount.
Practice Problems With Solutions
Easy Difficulty Level
Solve these basic percentage problems:
- What is 15% of 80?
- 12 is what percent of 60?
Medium Difficulty Level
Test your skills with these intermediate percentage questions:
- If a shirt costs $25 after a 20% discount, what was its original price?
- Find the percentage increase from 40 to 50.
Hard Difficulty Level
Challenge yourself with these complex percentage calculations:
- A company’s profits increased by 30% this year. If the profit last year was $50,000, what is the profit this year?
- How much 18% of 500 plus 25% of 200?
Frequently Asked Questions
1. What is the easiest way to calculate percentages?
The easiest way is by using the formula Part/Whole×100, ensuring you know both the part and the whole values.
2. How can I calculate percentage change between two values?
To calculate percentage change, subtract the original value from the new value, divide by the original value, and multiply by 100.
3. How do I convert a percentage into a fraction?
To convert a percentage into a fraction, divide the percentage by 100 and simplify the fraction if necessary.
4. How are percentages used in everyday life?
Percentages are used in sales, finance (interest rates), statistics, taxes, discounts, and education (grades).
5. Can I calculate percentages without a calculator?
Yes, by using basic arithmetic, you can calculate percentages mentally or by hand, although a calculator can speed up the process.
6. How do I find 1% of a number?
To find 1% of any number, divide the number by 100.
Summary
Understanding how to calculate percentage is an essential skill for everyday life. Whether it’s determining discounts during shopping or analyzing data in the professional realm, percentages play a crucial role. By grasping the simple formulas and methods outlined, you can confidently navigate through various percentage calculations with ease.







